- e หรือค่าคงตัวของออยเลอร์ เป็นค่าคงตัวทางคณิตศาสตร์ที่สำคัญค่าหนึ่ง มีค่าประมาณ 2.718 และเป็นฐานของลอการิทึมธรรมชาติ ใช้เป็นแนวทางนำไปสู่การนิยามการยกกำลังที่มีเลขชี้กำลังไม่เป็นจำนวนเต็ม ค่าคงตัวนี้นิยามโดยลิมิตต่อไปนี้ ซึ่งเลขชี้กำลังมีค่าเข้าใกล้อนันต์ในขณะที่ฐานมีค่าเข้าใกล้ 1
ฟังก์ชันเลขชี้กำลังซึ่งนิยามโดยลิมิตต่อไปนี้
มี x เป็นเลขชี้กำลังเพิ่มเข้ามา และสอดคล้องกับเอกลักษณ์การยกกำลัง
ฟังก์ชันเลขชี้กำลังนิยามขึ้นสำหรับ x ที่เป็นจำนวนเต็ม จำนวนตรรกยะ จำนวนจริง และจำนวนเชิงซ้อนทั้งหมด นอกจากนี้ก็สามารถขยายการยกกำลังไปบนสิ่งอื่นที่ไม่ใช่จำนวนได้เช่นเมทริกซ์จัตุรัส อย่างไรก็ตามเอกลักษณ์การยกกำลังที่ยกมาจะเป็นจริงก็ต่อเมื่อ x และ y สามารถสลับที่กันได้เท่านั้น
แสดงให้เห็นว่า ex+y สอดคล้องกับเอกลักษณ์การยกกำลังเมื่อ x และ y เป็นจำนวนเต็มบวก ผลจากการพิสูจน์ยังคงสอดคล้องสำหรับจำนวนทุกจำนวนด้วย ไม่เพียงแค่จำนวนเต็มบวก
เลขชี้กำลังเป็นจำนวนจริง
เนื่องจากจำนวนจริงสามารถประมาณค่าได้ด้วยจำนวนตรรกยะ การยกกำลังด้วยจำนวนจริง x ทุกจำนวนจึงสามารถนิยามได้ด้วยความต่อเนื่องด้วยกฎดังนี้
ลิมิตดังกล่าวซึ่ง r ที่มีค่าเข้าใกล้ x ถูกนำมาแทนที่เฉพาะจำนวนตรรกยะ r
ยกตัวอย่าง ถ้า
ดังนั้น
การยกกำลังด้วยจำนวนจริงโดยปกติก็สามารถทำให้สำเร็จได้ด้วยลอการิทึม แทนที่จะใช้ลิมิตของจำนวนตรรกยะ
ลอการิทึมธรรมชาติ ln(x) เป็นฟังก์ชันผกผันของฟังก์ชันเลขชี้กำลัง ex ซึ่งนิยามไว้สำหรับ b > 0 และสอดคล้องกับเงื่อนไข
ถ้า bx ถูกนิยามขึ้นโดยยังคงรักษากฎต่าง ๆ ของลอการิทึมและการยกกำลัง จะได้ว่า
สำหรับจำนวนจริง x แต่ละจำนวน
สิ่งนี้สามารถใช้เป็นนิยามทางเลือกของการยกกำลังด้วยจำนวนจริง bx และสอดคล้องกับวิธีการใช้เลขชี้กำลังเป็นจำนวนตรรกยะกับความต่อเนื่อง นิยามดังกล่าวเป็นวิธีการปกติสามัญในบริบทของจำนวนเชิงซ้อนอีกด้วย
รากที่ n ที่เป็นลบ
กำลังของจำนวนจริงบวกจะมีค่าเป็นจำนวนจริงบวกเสมอ อย่างไรก็ตาม คำตอบของสมการ x2 = 4 อาจเป็น 2 หรือ −2 ก็ได้ ค่ามุขสำคัญของ 41/2 คือ 2 แต่ −2 ก็เป็นรากที่สองที่ถูกต้องอีกค่าหนึ่งด้วย หากนิยามของการยกกำลังของจำนวนจริงขยายแนวคิดให้มีผลลัพธ์เป็นจำนวนลบได้ ผลของการยกกำลังอาจลักลั่น
ถ้า n เป็นจำนวนคู่ จากสมการ xn = a ถ้า a เป็นบวกจะมีสองคำตอบ ได้แก่รากที่ n ที่เป็นบวกและลบ แต่ถ้า a เป็นลบจะไม่มีคำตอบเป็นจำนวนจริง
ถ้า n เป็นจำนวนคี่ จากสมการ xn = a จะมีคำตอบที่เป็นจำนวนจริงหนึ่งจำนวน ถ้า a เป็นบวกก็จะได้คำตอบนั้นเป็นบวก และถ้า a เป็นลบก็จะได้คำตอบนั้นเป็นลบ
สำหรับเลขชี้กำลังที่เป็นจำนวนตรรกยะ m/n ในพจน์น้อยที่สุด ถ้า m เป็นจำนวนคู่ ผลลัพธ์จะเป็นบวก; ในกรณีที่ a เป็นลบ ถ้า m กับ n เป็นจำนวนคี่ ผลลัพธ์จะเป็นลบ; ในกรณีที่ a เป็นบวกและ n เป็นจำนวนคู่ ผลลัพธ์อาจเป็นบวกหรือลบอย่างใดอย่างหนึ่ง ตัวอย่างเช่น (−27)1/3 = −3, (−27)2/3 = 9, 43/2 มีสองคำตอบคือ 8 กับ −8 และเนื่องจากไม่มีจำนวนจริง x ที่ทำให้ x2 = −1 ดังนั้นนิยามของ am/n ในกรณีที่ a เป็นลบและ n เป็นจำนวนคู่ จึงจำเป็นต้องใช้หน่วยจินตภาพ i เข้ามาเกี่ยวข้อง
ไม่ว่าวิธีการใช้ลอการิทึมหรือเลขชี้กำลังเป็นจำนวนตรรกยะ ก็ไม่สามารถนิยาม ar ให้เป็นจำนวนจริงได้ สำหรับ a ที่เป็นจำนวนจริงลบและทุกช่วงค่าของจำนวนจริง r และทำนองเดียวกัน er ให้ผลลัพธ์เป็นบวกสำหรับทุกช่วงค่าของจำนวนจริง r ดังนั้น ln(a) ซึ่งเป็นฟังก์ชันผกผันจึงไม่อาจนิยามให้เป็นจำนวนจริงได้สำหรับ a ≤ 0 (ในทางตรงข้าม กำลังเชิงซ้อนของจำนวนลบ a สามารถนิยามได้ด้วยลอการิทึมเชิงซ้อนของ a)
วิธีการใช้เลขชี้กำลังเป็นจำนวนตรรกยะไม่สามารถใช้ได้กับค่า a ที่เป็นลบ เพราะวิธีการนี้ขึ้นอยู่กับความต่อเนื่อง หมายความว่า ฟังก์ชัน f(r) = arเป็นการขยายจำนวนตรรกยะไปเป็นจำนวนจริงอย่างต่อเนื่องเพียงหนึ่งเดียวเมื่อ a > 0 แต่ในกรณี a < 0 ฟังก์ชัน f ไม่ต่อเนื่องบนเซตของจำนวนจริง r ที่กำหนดไว้แต่ละค่า
ตัวอย่าง สมมติให้ a = −1 รากที่ n ของ −1 เท่ากับ −1 สำหรับจำนวนคี่บวก n ทุกจำนวน; แต่ถ้า n เป็นจำนวนคู่บวก (−1)(m/n) = −1 เมื่อ m เป็นจำนวนคี่, (−1)(m/n) = 1 เมื่อ m เป็นจำนวนคู่ ดังนั้นเซตของจำนวนตรรกยะ q ที่ทำให้ (−1)q = 1 เป็นเซตหนาแน่น (dense set) ในจำนวนตรรกยะ เช่นเดียวกับเซตของ q ที่ทำให้ (−1)q = −1 สิ่งนี้หมายความว่าฟังก์ชัน (−1)q ไม่ต่อเนื่องที่จำนวนตรรกยะ q ใด ๆ ที่กำหนดไว้แต่ละค่า
เมื่อใช้เอกลักษณ์การยกกำลังกับรากที่ n ที่เป็นลบ จำเป็นต้องระวัดระวังเป็นพิเศษ ตัวอย่างเช่น −27 = (−27)((2/3)×(3/2)) = ((−27)2/3)3/2 = 93/2 = 27 ซึ่งผิดอย่างชัดเจน ปัญหาอยู่ที่การใช้รากที่สองที่เป็นบวก แทนที่จะใช้รากที่สองที่เป็นลบในขั้นตอนสุดท้าย แต่โดยทั่วไปปัญหาที่คล้ายกันนี้มักเกิดขึ้นกับจำนวนเชิงซ้อน ดังที่ได้อธิบายไว้ในหัวข้อความผิดพลาดของเอกลักษณ์กำลังและลอการิทึม
กำลังจำนวนเชิงซ้อนของจำนวนจริงบวก
กำลังจำนวนจินตภาพของ e
- การทำความเข้าใจ eix สำหรับจำนวนจริง x ต้องทราบถึงการแปลความหมายเชิงเรขาคณิตของการดำเนินการบนจำนวนเชิงซ้อน และนิยามกำลังของ e ดังที่กล่าวไว้แล้วข้างต้น พิจารณารูปสามเหลี่ยมมุมฉาก (0, 1, 1 + ix/n) สำหรับจำนวน n ที่มีขนาดใหญ่มาก ๆ รูปสามเหลี่ยมนั้นจะมีลักษณะเข้าใกล้เซกเตอร์ของรูปวงกลมมากยิ่งขึ้น โดยมีมุมที่จุดศูนย์กลางเท่ากับ x/n เรเดียน และรูปสามเหลี่ยมอื่น ๆ (0, (1 + ix/n)k, (1 + ix/n)k+1) ก็เป็นรูปสามเหลี่ยมคล้ายร่วมกันสำหรับ k ทุกค่า เพราะฉะนั้น สำหรับจำนวน n ขนาดใหญ่ จุดที่เป็นขอบเขตของ (1 + ix/n)n ก็คือจุดที่อยู่บนรูปวงกลมหนึ่งหน่วย ซึ่งมุมที่วัดจากแกนจำนวนจริงบวกเท่ากับ x เรเดียน พิกัดเชิงขั้วของจุดนี้คือ (r, θ) = (1, x) และพิกัดคาร์ทีเซียนคือ(cos x, sin x) ดังนั้นในท้ายที่สุด eix = cos x + i sin x เรียกว่าสูตรของออยเลอร์ ซึ่งเชื่อมโยงพีชคณิตกับตรีโกณมิติด้วยความหมายของจำนวนเชิงซ้อน
คำตอบของสมการ ez = 1 คือพหุคูณจำนวนเต็มของ 2πi
ในกรณีทั่วไป ถ้ากำหนดให้ eb = a ดังนั้นคำตอบของสมการ ez = a หาได้โดยการบวกb เข้ากับพหุคูณจำนวนเต็มของ 2πi
ดังนั้นฟังก์ชันเลขชี้กำลังเชิงซ้อนเป็นฟังก์ชันเป็นคาบ (periodic function) ซึ่งมีคาบเท่ากับ 2πi
นอกจากนี้ก็ยังมีสูตรอื่น ๆ อีกเช่น eiπ = −1; ex + iy = ex(cos y + i sin y)
ฟังก์ชันตรีโกณมิติ
- จากการแปลงสูตรของออยเลอร์ ฟังก์ชันตรีโกณมิติ โคไซน์และไซน์ถูกแปลงเป็น
โคไซน์และไซน์ถูกนิยามขึ้นโดยทางเรขาคณิตก่อนมีการประดิษฐ์จำนวนเชิงซ้อนในประวัติศาสตร์ สูตรทั้งสองด้านบนเป็นการลดรูปสูตรที่ซับซ้อนของฟังก์ชันตรีโกณมิติของผลบวกเป็นสูตรการยกกำลังอย่างง่ายว่า
การใช้การยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเชิงซ้อน อาจช่วยลดรูปปัญหาในตรีโกณมิติไปเป็นพีชคณิตได้
กำลังจำนวนเชิงซ้อนของ e
การยกกำลัง z = ex+i·y สามารถคำนวณได้จาก ex · ei·y; ตัวประกอบส่วนจริง ex คือค่าสัมบูรณ์ของ z และตัวประกอบส่วนจินตภาพ ei·yระบุทิศทางของ z
กำลังจำนวนเชิงซ้อนของจำนวนจริงบวก
กำหนดให้ a เป็นจำนวนจริงบวก และ z เป็นจำนวนเชิงซ้อนใด ๆ การยกกำลัง az นิยามโดย ez·ln(a) เมื่อ x = ln(a) เป็นคำตอบจำนวนจริงเพียงหนึ่งเดียวของสมการ ex = a ดังนั้นวิธีการเดียวกันที่ใช้กับเลขชี้กำลังจำนวนจริงก็ยังคงใช้ได้กับเลขชี้กำลังจำนวนเชิงซ้อน ตัวอย่างเช่น
-
- 2i = e i·ln(2) = cos(ln(2)) + i·sin(ln(2)) ≈ 0.76924 + 0.63896i
- ei ≈ 0.54030 + 0.84147i
- 10i ≈ −0.66820 + 0.74398i
- (e2π)i ≈ 535.49i ≈ 1
กำลังของจำนวนเชิงซ้อน
กำลังจำนวนเต็มของจำนวนเชิงซ้อนที่ไม่เป็นศูนย์นิยามโดยการคูณหรือการหารซ้ำ ๆ เช่นเดียวกับที่ได้กล่าวแล้ว ถ้า i คือหน่วยจินตภาพและ n คือจำนวนเต็มแล้ว in จะมีค่าเท่ากับ 1, i, −1 หรือ −i ขึ้นอยู่กับค่า n ว่าสมภาคกับ 0, 1, 2 หรือ 3 มอดุโล 4 ตามลำดับ (หรืออีกนัยหนึ่งคือ n หารด้วย 4 แล้วเหลือเศษเท่าใด) ด้วยสาเหตุนี้ กำลังของ i จึงมีประโยชน์ในการเขียนแทนลำดับที่มีคาบแบ่งเป็น 4 ช่วง
กำลังจำนวนเชิงซ้อนของจำนวนจริงบวกได้นิยามผ่านทาง ex ตามที่อธิบายไว้ในหัวข้อกำลังจำนวนเชิงซ้อนของจำนวนจริงบวก ซึ่งเป็นฟังก์ชันต่อเนื่อง
การขยายแนวคิดของฟังก์ชันเหล่านี้ไปเป็นกรณีทั่วไปคือ กำลังที่ไม่เป็นจำนวนเต็มของจำนวนเชิงซ้อนที่ไม่ใช่จำนวนเต็มบวก ทำให้เกิดความยุ่งยาก นั่นคือต้องนิยามฟังก์ชันไม่ต่อเนื่องหรือฟังก์ชันหลายค่าอย่างใดอย่างหนึ่ง แต่ไม่ว่าทางเลือกใดก็ไม่สามารถนิยามให้สอดคล้องเพียงพอทั้งหมดได้
กำลังจำนวนตรรกยะของจำนวนเชิงซ้อนต้องเป็นคำตอบของสมการเชิงพีชคณิตสมการหนึ่ง ดังนั้นมันจึงมีคำตอบที่เป็นไปได้จำนวนจำกัดหนึ่งเสมอ ตัวอย่างเช่น w = z1/2 ต้องเป็นคำตอบของสมการ w2 = z แต่เมื่อ w เป็นคำตอบแล้ว −w ก็เป็นคำตอบด้วยเช่นกันเพราะว่า (−1)2 = 1 คำตอบเพียงหนึ่งเดียวที่ถูกเลือกโดยค่อนข้างปราศจากเหตุผลเรียกว่าค่ามุขสำคัญ (principal value) สามารถเลือกโดยใช้กฎทั่วไปซึ่งใช้กับกำลังที่ไม่ใช่จำนวนตรรกยะด้วย
กำลังและลอการิทึมเชิงซ้อนโดยธรรมชาติถือว่าเป็นฟังก์ชันค่าเดียวบนผิวรีมันน์ (Riemann surface) รูปแบบค่าเดียวถูกนิยามขึ้นโดยการเลือกผิวขึ้นมาอันหนึ่ง ค่าของมันไม่มีความต่อเนื่องตามแนวส่วนตัดกิ่ง (branch cut) การเลือกหนึ่งคำตอบจากหลายคำตอบเป็นค่ามุขสำคัญก็ยังคงได้ฟังก์ชันที่ไม่มีความต่อเนื่อง และกฎต่าง ๆ ที่ใช้จัดการกับการยกกำลังตามปกติอาจนำไปสู่ความผิดพลาดได้
กำลังจำนวนอตรรกยะของจำนวนเชิงซ้อนมีคำตอบที่เป็นไปได้ไม่จำกัด เพราะธรรมชาติของลอการิทึมเชิงซ้อนสามารถมีคำตอบได้หลายค่า ค่ามุขสำคัญคือค่าค่าหนึ่งที่ถูกเลือกด้วยกฎอย่างหนึ่งท่ามกลางคุณสมบัติอื่น ๆ ที่ทำให้แน่ใจว่า กำลังของจำนวนเชิงซ้อนที่มีส่วนจริงเป็นบวกและส่วนจินตภาพเป็นศูนย์ จะมีค่าเหมือนกับกำลังของจำนวนจริงที่เกี่ยวข้อง
การยกกำลังจำนวนจริงด้วยจำนวนเชิงซ้อนเป็นการดำเนินการที่แตกต่างจากการยกกำลังจำนวนเชิงซ้อนที่เกี่ยวข้อง อย่างไรก็ตามในกรณีของจำนวนจริงบวก ค่ามุขสำคัญนั้นเหมือนกัน
กำลังของจำนวนจริงลบนั้นไม่ได้ถูกนิยามเสมอไป และไม่ต่อเนื่องแม้ว่าจะได้นิยามแล้ว ดังนั้นเมื่อพบกับจำนวนเชิงซ้อน ควรใช้การดำเนินการสำหรับจำนวนเชิงซ้อนแทน
กำลังจำนวนเชิงซ้อนของจำนวนเชิงซ้อน
สำหรับจำนวนเชิงซ้อน a และ b ซึ่ง a ≠ 0 สัญกรณ์ ab เกิดความกำกวมในคำตอบเหมือนกับ log a
เพื่อหาค่าของ ab ขั้นตอนแรกจะต้องเลือกลอการิทึมของ a ขึ้นมาค่าหนึ่ง ทางเลือกนั้นอาจเป็น Log a (คือค่ามุขสำคัญของ log a โดยปริยายหากมิได้กำหนดเงื่อนไขอื่นเพิ่ม) หรืออาจเป็นค่าหนึ่งจากกิ่งอื่นของ log z ที่กำหนดตายตัว ดังนั้นจึงสามารถนิยามโดยใช้ฟังก์ชันลอการิทึมเชิงซ้อนดังนี้
เพราะนิยามนี้สอดคล้องกับนิยามที่ให้ไว้ก่อนหน้านี้ ในกรณีที่ a เป็นจำนวนจริงบวกและค่ามุขสำคัญของ log a (ซึ่งเป็นจำนวนจริง) ได้ถูกเลือก
ถ้า b เป็นจำนวนเต็ม ดังนั้นค่าของ ab จะไม่ขึ้นอยู่กับตัวเลือกของ log a เพราะสอดคล้องกับนิยามการยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็ม
ถ้า b เป็นจำนวนตรรกยะ m/n ในพจน์น้อยที่สุดโดยที่ n > 0 ดังนั้นจะมีตัวเลือกของ log a เป็นจำนวนไม่จำกัดให้ค่าที่แตกต่างกัน n จำนวนสำหรับ abซึ่งค่าเหล่านี้คือจำนวนเชิงซ้อน z ที่เป็นคำตอบของสมการ zn = am
ถ้า b เป็นจำนวนอตรรกยะ ดังนั้นจะมีตัวเลือกของ log a เป็นจำนวนไม่จำกัด นำไปสู่ค่าของ ab ที่แตกต่างกันเป็นจำนวนไม่จำกัดเช่นกัน
การคำนวณกำลังจำนวนเชิงซ้อนสามารถทำให้ง่ายขึ้นโดยการแปลงฐาน a เป็นรูปแบบเชิงขั้ว ดังที่อธิบายไว้ด้านล่าง การสร้างที่คล้ายก็สามารถใช้ควอเทอร์เนียน (quaternion) ได้ด้วย
รากเชิงซ้อนของ 1 (รากปฐมฐาน)
- ดูบทความหลักที่ รากของ 1
จำนวนเชิงซ้อน a ที่ทำให้ an = 1 สำหรับจำนวนเต็มบวก n เรียกว่า รากที่ n ของ 1 (nth root of unity) หรือเรียกสั้น ๆ ว่า รากของ 1 (root of unity) รากเหล่านี้มี n คำตอบและวางตัวคล้ายจุดยอดของรูป n เหลี่ยมปรกติ บนรูปวงกลมหนึ่งหน่วยบนระนาบเชิงซ้อน ซึ่งมีจุดยอดจุดหนึ่งอยู่ที่จำนวนจริง 1
ถ้า zn = 1 แต่ zk ≠ 1 สำหรับจำนวนธรรมชาติ k ตามเงื่อนไข 0 < k < n แล้ว z จะเรียกว่า รากปฐมฐานที่ n (primitive nth root of unity) ตัวอย่างเช่น −1 เป็นรากปฐมฐานที่สองเพียงตัวเดียว, รากปฐมฐานที่สี่มีสองตัวได้แก่ i และ −i (ไม่นับรากปฐมฐานที่สอง) เป็นต้น
จำนวน e2πi (1/n) คือรากปฐมฐานที่ n ที่มีอาร์กิวเมนต์เป็นบวกน้อยที่สุด (บางครั้งอาจเรียกว่า รากปฐมฐานที่ n "มุขสำคัญ" ถึงแม้ว่าการใช้คำนี้จะไม่แพร่หลายและอาจทำให้สับสนกับ ค่ามุขสำคัญของรากที่ n ของ 1 ซึ่งหมายถึงค่า 1)
ส่วนรากของ 1 จำนวนอื่น ๆ คำนวณได้จาก
สำหรับ 2 ≤ k ≤ n
รากของจำนวนเชิงซ้อนโดยทั่วไป
แม้ว่าลอการิทึมเชิงซ้อนมีค่าที่เป็นไปได้มากมายไม่จำกัด แต่ก็มีค่าเป็นจำนวนจำกัดเท่านั้นที่เป็นคำตอบของ az โดยเฉพาะในกรณีที่ z = 1/n และ nเป็นจำนวนเต็มบวก ค่าเหล่านี้คือรากที่ n ของ a ซึ่งเป็นคำตอบของสมการ xn = a
ในทางคณิตศาสตร์ เราอาจทำให้การคำนวณสะดวกขึ้นโดยนิยาม a1/n ให้เป็นค่ามุขสำคัญของราก ถ้า a เป็นจำนวนจริงบวก จะสามารถเลือกคำตอบเป็นจำนวนจริงบวกเป็นค่ามุขสำคัญได้อย่างง่ายดาย สำหรับจำนวนเชิงซ้อนโดยทั่วไป รากที่ n ที่มีอาร์กิวเมนต์น้อยที่สุดมักจะถูกเลือกเป็นค่ามุขสำคัญของราก เช่นเดียวกับค่ามุขสำคัญของรากของ 1
เซตของรากที่ n ของจำนวนเชิงซ้อน a หาได้จากการคูณค่ามุขสำคัญของ a1/n ด้วยรากที่ n ของ 1 แต่ละจำนวน ตัวอย่างเช่น รากที่สี่ของ 16 ได้แก่ 2, −2, 2i และ −2i เพราะว่าค่ามุขสำคัญของรากที่สี่ของ 16 คือ 2 และรากที่สี่ของ 1 ได้แก่ 1, −1, i และ −i
การคำนวณกำลังจำนวนเชิงซ้อน
การคำนวณกำลังจำนวนเชิงซ้อนสามารถทำได้ง่ายขึ้นโดยเขียนเป็นการยกกำลังในรูปแบบเชิงขั้ว จำนวนเชิงซ้อน z ทุกจำนวนสามารถเขียนให้อยู่ในรูปแบบเชิงขั้วดังนี้
เมื่อ r คือจำนวนจริงไม่เป็นลบและ θ คืออาร์กิวเมนต์ของ z (ซึ่งเป็นจำนวนจริง) รูปแบบเชิงขั้วมีการแปลความหมายเชิงเรขาคณิตว่า ถ้าจำนวนเชิงซ้อน u+ iv แทนได้ด้วยจุด (u, v) บนระนาบเชิงซ้อนโดยระบบพิกัดคาร์ทีเซียน ดังนั้น (r, θ) ก็คือจุดเดียวกันในระบบพิกัดเชิงขั้ว นั่นหมายความว่า r คือ "รัศมี" ที่มีค่าตาม r2 = u2 + v2 และ θ คือ "มุม" ที่มีค่าตาม θ = atan2(v, u) (ฟังก์ชัน atan2 มาจากฟังก์ชัน arctan ที่มีเงื่อนไขเพิ่มเติม) มุมเชิงขั้ว θ มีความกำกวมเนื่องจาก θ สามารถบวกด้วยพหุคูณใด ๆ ของ 2π แล้วไม่ทำให้จุดเปลี่ยนตำแหน่งไปจากเดิม ตัวเลือกแต่ละค่าของ θ โดยทั่วไปจะให้ผลการยกกำลังที่แตกต่างกัน ส่วนตัดกิ่งส่วนหนึ่งสามารถนำมาใช้เพื่อเลือกค่าที่เจาะจง ค่ามุขสำคัญ (ส่วนตัดกิ่งที่สามัญที่สุด) สอดคล้องกับ θ ที่ถูกเลือกในช่วงค่า (−π, π] สำหรับจำนวนเชิงซ้อนที่มีส่วนจริงเป็นบวกและส่วนจินตภาพเป็นศูนย์ซึ่งใช้ค่ามุขสำคัญเช่นนั้น จะให้ผลลัพธ์เดียวกับการใช้จำนวนจริงที่เกี่ยวข้อง
เพื่อที่จะคำนวณกำลังเชิงซ้อน ab ขั้นแรกเขียน a ในรูปแบบเชิงขั้ว
ดังนั้น
และจะได้
ถ้า b ถูกแบ่งออกเป็น c + di ดังนั้นสูตรสำหรับ ab จึงเขียนให้ชัดเจนยิ่งขึ้นได้เป็น
สูตรสุดท้ายนี้ช่วยคำนวณการยกกำลังจำนวนเชิงซ้อนได้โดยง่าย จากการแบ่งฐานกับเลขชี้กำลังออกเป็นรูปแบบเชิงขั้วกับรูปแบบคาร์ทีเซียนตามลำดับ สูตรดังกล่าวแสดงผลลัพธ์ทั้งรูปแบบเชิงขั้วและรูปแบบคาร์ทีเซียน (ผ่านทางเอกลักษณ์ของออยเลอร์)
ตัวอย่างต่อไปนี้จะใช้ค่ามุขสำคัญคือส่วนตัดกิ่งที่ทำให้ θ อยู่ในช่วงค่า (−π, π] กำหนดโจทย์ i i ขั้นแรกเขียน i ในรูปแบบเชิงขั้วและรูปแบบคาร์ทีเซียนดังนี้
จากการแปลงด้านบน จะได้ว่า r = 1, θ = π/2, c = 0 และ d = 1 ดังนั้น
เช่นเดียวกันสำหรับโจทย์ (−2)3 + 4i หารูปแบบเชิงขั้วของ −2 ได้เป็น
แล้วใช้สูตรด้านบนคำนวณจนได้คำตอบ
ค่าของการยกกำลังจำนวนเชิงซ้อนขึ้นอยู่กับกิ่งที่เลือก ตัวอย่างเช่น ถ้าเลือกรูปแบบเชิงขั้วของ i = 1ei (5π/2) เพื่อคำนวณ i i คำตอบจะกลายเป็น e−5π/2แต่ค่ามุขสำคัญของ i i คือ e−π/2 ดังตัวอย่างที่แสดงไว้แล้ว เซตของค่าทั้งหมดที่เป็นไปได้สำหรับ i i สามารถหาได้จากเงื่อนไข
เมื่อ k เป็นจำนวนเต็มจำนวนหนึ่ง ดังนั้นคำตอบที่เป็นไปได้ของ i i จึงมีจำนวนไม่จำกัดสำหรับค่า k แต่ละค่า คำตอบทั้งหมดมีส่วนจินตภาพเป็นศูนย์ ดังนั้นเราจึงอาจกล่าวได้ว่า i i มีค่าเป็นจำนวนจริงและมีเป็นอนันต์
ที่มา:th.wikipedia.org/wiki/การยกกำลัง





![5^x \approx 5^{1.732} = 5^{433/250} = \sqrt[250]{5^{433}} \approx 16.241](http://upload.wikimedia.org/wikipedia/th/math/c/0/9/c09a8e4fe72ee9e5630b6ca35e726d49.png)






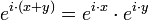







![\left( r^c e^{-d\theta} \right) e^{i (d \log r + c\theta)} = \left( r^c e^{-d\theta} \right) \left[ \cos(d \log r + c\theta) + i \sin(d \log r + c\theta) \right]](http://upload.wikimedia.org/wikipedia/th/math/e/d/1/ed138a9e61a6015c1ec748eeba11ff03.png)



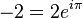


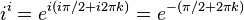
ไม่มีความคิดเห็น:
แสดงความคิดเห็น